Variation in data over the limits of datatypes

Every basic datatype is allocated with predefined size. Based upon the memory allocated, the range of values stored in a variable of particular datatype varies. Operations on the variables are smooth when they are within the lower and upper limits of these datatypes. It is ambiguous to guess the output when operations are being performed across the lower and upper limits, and vice versa.

Execute the following program and checkout the result.

 #include<stdio.h>  
 main()  
 {  
  char ch=127;  
  ch++;  
  printf("%d\n",ch);//printf("%c\n",ch);  
 }  

 #include<stdio.h>  
 main()  
 {  
  unsigned int i=-1;  
  i--;  
  printf("%d\n",i);  
 }  

Note that though ‘char’ is the datatype capable of storing characters and special symbols, internally it is considered as integer based upon the ASCII values and we can assign integer values to ‘char’ variables as shown. You can check the ASCII values in the manual page – man ascii

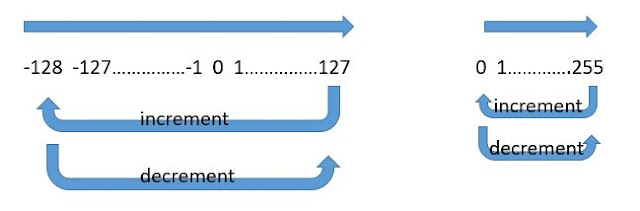
We know that gcc allocates 1byte of memory for a ‘char’ variable i.e., 8 bits. With these 8 bits, the char datatype is capable of storing 0-255 range of values. We know that the MSB of a byte is used for sign of the data stored in it. Hence, the range 0-255 (for unsigned char) changes from -128 to +127 (for signed char). All the ASCII values are stored from 0-127. Any value beyond this range produces unexpected results.

First, we have ch=127. Generally, when 127 is incremented by 1, it should be 128. But, the upper limit overflows to the lower limit as shown below. The same way, when the lower limit -128 is decremented by 1, it shows up with the value 128.

Data overflow in char datatype

In the case of unsigned char, the lower limit becomes 0 and the upper limit becomes 255. The upper limit overflow navigates to the lower limit and the lower limit overflow results in the value shift to upper limit.

In simple words to say, the upper and lower limit overflow is circular – lower limit overflow results in a shift to upper limit and the upper limit over flow results in a shift to lower limit.

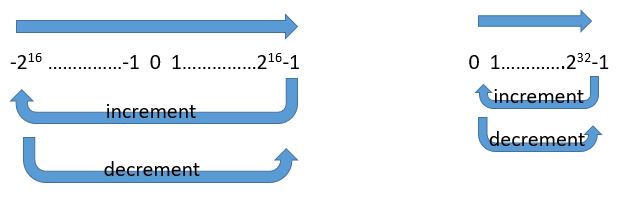
Till now, we illustrated how data overflows over the limits for ‘char’ datatype, which is 1byte in size. The same can be applied to integer also, with a catch that ‘int’ is of 4 bytes size in gcc. With 4 bytes, it is 32bits. Hence, the range of signed int is -2¹⁶ to 2¹⁶-1 and that of signed is 0 to 2³²-1. When the vaule 2¹⁶-1 is incremented by 1, it moves to -2¹⁶ and when the value -2¹⁶ is decremented by 1, it moves to 2¹⁶, for signed int. For unsigned int, 0 when decremented by 1 becomes 2³²-1 and when 2³²-1 is incremented by 1 becomes 0. Checkout the outputs of the following programs so that you can get a clear idea how data overflows at the boundaries.

 #include<stdio.h>  
 main()  
 {  
  int i=-1;//compiler takes int as signed int by default  
  i--;  
  printf("%d\n",i);  
 }  

Also, note that the same pattern of overflow occurs for all the integral datatypes.

Data overflow in int datatype

The overflow pattern differs for real datatypes. Before that one needs know how float data is stored in the memory. IEEE 754 standard defined floating point storage. Every real data has 3 parts and they differ from float to double as shown below.

Floating point data storage

The keywords ‘signed’ and ‘unsigned’ are called sign qualifiers. There is no concept of sign qualifiers in real data. The sign is automatically stored in the MSB, as shown below.

IEEE 754 format for real data

How to convert float value to binary value?

Now, let us see how the values are stored in the sign, exponent and mantissa for a given real value. For example, let us convert 23.4 floating value to binary.

(23)₁₀ = (10111)₂

0.4 can be converted to binary as shown below.

0.4 x 2 = 0.8 -> 0

0.8 x 2 = 1.6 -> 1

1.6 x 2 = 1.2 -> 1

0.2 x 2 = 0.4 -> 0

0. 4 x 2 = 0.8 (recurring)

(0.4)10 = 0.01100110……..(recurring)

Now, (23.4)₁₀ = (10111.01100110….)₂

                           = 1.011101100110…..E+4

In the resultant binary representation, as the result is +ve, the sign bit is stored with 0, the bits after decimal point are stored in mantissa and +4 is the exponent. But, it is stored as 127+4, which is 10000011 in binary. Now, all these three parts are stored into memory as shown below.

Example for IEEE 754: 23.4 floating point storage in binary format

For double datatype, the exponent is stored as 1023+4.

increment or decrement operators show their effect only on the integral part of the floating point. For example, see the following program and check the output.

 #include<stdio.h>  
 main()  
 {  
  float f=1.23;  
  f++;  
  printf("%f\n",f);  
 }  

Overflow of data does not occur in real datatypes, unless it is intended to occur. So, there is no need to bother about how data varies over the limit in real datatypes, as we have infinite number of floating points between two given numbers.

Also, check the output of the program mentioned below, so that you can get a clear idea about floating points. Note that %e is used to display a floating point in exponential format.

 #include<stdio.h>  
 main()  
 {  
  float v=25.25;  
  printf("%f\n",v);  
  printf("%e\n",v);  
  v=12345.6;  
  printf("%f\n",v);  
  printf("%e\n",v);  
 }